Taylor Series Woes

Note: I still hate Mathematica. It swallows signs of certain expressions, it eats my files, and itgets units wrong. I hate to use it. But for quick hacks like the following, it's a nice tool.

I wanted to find a simplification for the following formula:

amp = amp0/(omega0^2 - omega^2 + I gamma omega)

(If you're wondering: the formula gives the amplitude term of the driven, damped, harmonic oscillator.)

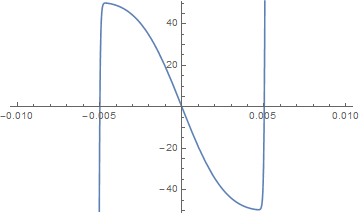
Specifically, I was interested in the real part of this amplitude term around the center of the resonance:

simple1 = Re[amp] /. omega -> omega0 + eps // ComplexExpand // Simplify
params = {amp0 -> 1, gamma -> 0.01, omega0 -> 1};
Plot[Re[simple1 /. params], {eps, -0.01, 0.01}, 
PlotRange -> {-51, 51}]

I thought, surely I can estimate this as a Taylor series! Looking at the plot, third order should work nicely.

simple2 = 
 Re[amp] /. omega -> omega0 + eps // ComplexExpand // 
    Series[#, {eps, 0, 3}] & // Normal // Collect[#, eps, Simplify] &
Plot[Re[simple2 /. params], {eps, -0.01, 0.01}, 
 PlotRange -> {-51, 51}]

Hmm, not so nice. Obviously I need more terms. 100 should be enough.

simple3 = 
 Re[amp] /. omega -> omega0 + eps // ComplexExpand // 
    Series[#, {eps, 0, 100}] & // Normal // Collect[#, eps, Simplify] &
Plot[Re[simple2 /. params], {eps, -0.01, 0.01}, 
 PlotRange -> {-51, 51}]

At this point I vaguely started remembering words of caution about Taylor series, with terms such as convergence radius being thrown around... I guess this is one example where the Taylor series will only get you so far (in this case, just about to the extrema). Tayloring sqrt(x) around 0 being another pathological (but quite obvious) example. Back in the day (TM), during math classes, these examples were all over the place. But having done physics for so long, it's strange to come upon a real-life case where the Taylor series fails.

For what it's worth, a better approximation of the real part of the amplitude term is

simple4 = -(2 amp0 eps)/(4 eps^2 omega0 + gamma^2 omega0)