Confidence Band in a Matlab Fit

Fitting in Matlab

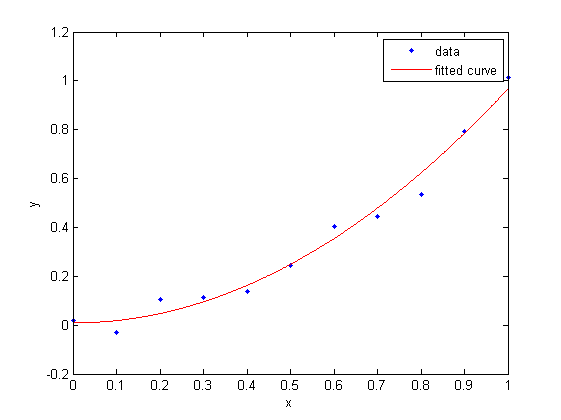
In Matlab, you can fit noisy data using the curve fitting toolbox. Example:

xdata = (0:0.1:1)';               % column vector!
noise = 0.1*randn(size(xdata));
ydata = xdata.^2 + noise;
f = fittype('a*x.^2 + b'); 
fit1 = fit(xdata, ydata, f, 'StartPoint', [1,1])
plot(fit1, xdata, ydata)

Side note: plot() is not our usual plot function, but a method of the cfit-object fit1.

Our fit uses the data to determine the coefficients $a,b$ of the underlying model $f(x) = a x^2 + b$. We can read out the uncertainty of the coefficients (the "confidence interval" of the coefficients) into a matrix. Each column(!) of the matrix corresponds to one coefficient, with the coefficients alphabetically ordered.

names = coeffnames(fit1)   % check the coefficient order!
ci = confint(fit1, 0.68);  % 1 sigma interval
a_ci = ci(:,1)
b_ci = ci(:,2)

By default, Matlab uses $2 \sigma$ (0.95) confidence intervals. As a physicist, make sure to specify $1 \sigma$ (0.68) intervals.

Confidence and Prediction Bands

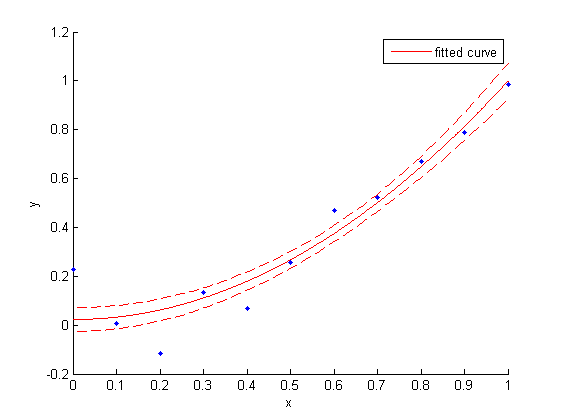
The confidence intervals of the coefficients do not tell the whole story - especially when the coefficients are correlated! A good visualisation of this case is to plot confidence bands or prediction bands around our data.

• Prediction band: If I take a new measurement value, where would I expect it to lie? In Matlab terms, this is called the "observation band".
• Confidence band: Where do I expect the true value to lie? In Matlab terms, this is called the "functional band".

As with the coefficient's confidence intervals, Matlab uses $2 \sigma$ bands by default, and you should switch it to $1 \sigma$ intervals. By its nature, the prediction band is bigger, because it comprises the uncertainty of the model (the confidence band!) and the scatter of the measurement.

There is a another destinction to make, one that I don't fully understand. Both Matlab and Wikipedia make that distinction.

• Pointwise: How big is the prediction/confidence band for a single measurement/true value? In virtually all cases I can think of, this is what you would want to ask as a physicist.
• Simultaneous: How big do you have to make the prediction/confidence band if you want a set of all new measurements/all prediction points to lie within the band with a given confidence?

In my personal opinion, the "simultaneous band" is not a band! For a measurement with $n$ points, it should be $n$ individual error bars!

The prediction/confidence distinction and the pointwise/simultaneous distinction give you a total of four options for "the" band around the plot. Matlab makes the $2 \sigma$ pointwise prediction band easily accessible, but what I am usually interested in is the $1\sigma$ pointwise confidence band. It is a bit more cumbersome to plot, because you have to specify dummy data over which to evaluate the prediction band:

x_dummy = linspace(min(xdata), max(xdata), 100);
figure(1); clf(1);
hold all
plot(xdata,ydata,'.')
plot(fit1)    % by default, evaluates the fit over the currnet XLim
% use "functional" (confidence!) band; use "simultaneous"=off
conf1 = predint(fit1,x_dummy,0.68,'functional','off');
plot(x_dummy, conf1, 'r--')
hold off

Note that the confidence band at $x=0$ equals the confidence interval of the fit-coefficient $b$!

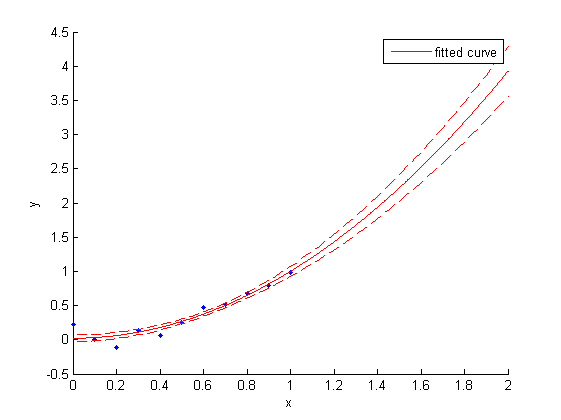
Extrapolation

If you want to extrapolate to x-values that are not covered by the range of your data, you can evaluate the fit and the prediction/confidence band for a bigger range:

x_range = [0, 2];
x_dummy = linspace(x_range(1), x_range(2), 100);
figure(1); clf(1);
hold all
plot(xdata,ydata,'.')
xlim(x_range)
plot(fit1)
conf1 = predint(fit1,x_dummy,0.68,'functional','off');
plot(x_dummy, conf1, 'r--')
hold off

Green's Functions Explained

General Idea

Suppose you want to find $f(x)$ that satisfies some linear, differential equation

$L\,f(x) = u(x),$

where $L$ is a linear differential operator and $u(x)$ some given function (the inhomogeneous term of the differential equation). The Green's function $G(x, x_0)$ can help you find the solution. $G$ is a function of two variables, and it satisfies the equation

$L\,G(x, x_0) = \delta(x - x_0).$

If you happen find $G(x, x_0)$, then you can multiply this equation by $u(x_0)$ and integrate over $x_0$:

$\int dx_0\,L\,G(x, x_0) u(x_0) = \int dx_0\,\delta(x-x_0)u(x_0).$

Rearrange the terms and you end up with

$L \int dx_0 G(x, x_0) u(x_0) = u(x).$

This solves your initial problem, because you can identify

$f(x) = \int dx_0 G(x, x_0) u(x_0).$

In the real world, you often deal with differential equations that have boundary conditions, for instance the electric potential must be 0 on the boundary. Green's functions are a great tool for these problems, because if the Green's function is 0 on the boundary, then any integral over Green's functions will also be 0 on the boundary. Conceptually, this is very similar to finding the image charge for any single charge within your boundary.

Completely Useless Example

Typical problem in electrostatics: Point charge in vacuum. (I left out all units). I'm including this because I first made a mistake when assigning a name to the location of the point charge. You must not name this $x_0$ and then integrate over $x_0$!

$\Delta \Phi(x) = \rho(x) = -\frac{1}{4\pi} \delta(x - x_p)$

Everyone "knows" that the solution is

$\Phi(x) = \frac{1}{\|x - x_p\|}$.

To find it with Green's function: Solve

$\Delta G(x,x_0) = \delta(x - x_0)$

Obviously, we know

$G(x,x_0) = \frac{1}{\|x - x_0\|}.$

To find the solution, calculate

$\Phi(x) = \int dx_0 G(x, x_0) \rho(x_0)\\ = \int dx_0 \delta(x - x_0) \frac{-1}{4\pi} \delta(x_0 - x_p)\\ = \frac{1}{\|x - x_p\|}$

Simple, useful example: Undamped, harmonic oscillator

Consider the harmonic oscillator forced by a function $u(x)$:

$f''(x) + \omega^2 f(x) = u(x)\\ \Rightarrow L = \frac{d^2}{dx^2} + \omega^2$

So we are looking for a function $G(x, x_0)$ that satisfies

$L\,G(x,x_0) = \delta(x-x_0)\quad.$

The corresponding physics case to this equation is a harmonic oscillator that is "bumped" at $x = x_0$. One solution that should work is

$G(x, x_0) = \begin{cases} 0 &\text{if } x < x_0 \\ A \sin(\omega x - \omega x_0) &\text{if } x \geq x_0 \end{cases}$

Or, using the Heaviside step function $\Theta(x)$, which I find easier to handle when doing derivatives:

$G(x,x_0) = A\,\Theta(x-x_0)\, \sin(\omega x - \omega x_0)$

We can prove that this is the right equation by showing that it holds true for $x < x_0$ (trivial), for $x > x_0$ (almost as trivial), and for:

$\int_{x_0 - a}^{x_0+a}\! G(x, x_0)\,dx = 1 \quad \forall \, a \quad .$

The last part is the only one that is a bit tricky, but you can quickly work out that the second derivative of $\Theta(x) \sin(x)$ is basically $\delta(x)$. In our case, the factor $A$ works out to $A = 1/\omega$.

It is quite easy to go to the damped harmonic oscillator from here. Just ask yourself "What does my system do when I poke it at $x = x_0$ with a $\delta$-pulse?", use that as a guess for $G(x,x_0)$, and find the factor $A$ of the solution.

Using Assumptions in Mathematica

Use Assumptions to simplify/modify terms. For example

Simplify[Sqrt[x^2]]

returns

Sqrt[x^2]

because x might be negative, in which case the expression cannot be simplified any further.

Mathematica keeps track of global assumptions in the variable (or whatever that is) $Assumptions. By default, this just contains True. If no other information is given, Mathematica assumes all variables to be complex.

If you are sure that x is real and positive, you can pass that information as an assumption to Simplify[] and related commands. The following three examples are roughly equivalent.

Simplify[Sqrt[x^2], Assumptions -> x > 0] 
Simplify[Sqrt[x^2], x > 0]
Assuming[x > 0, Simplify[Sqrt[x^2]]]

The difference between the three examples above is: The 1st example uses only the assumption that is given and ignores global $Assumptions. The 2nd and 3rd example use the given assumption in addition to global $Assumptions.

Of course, you can also modify the global assumptions. This can save you lots of typing.

$Assumptions = {x>0, y>0}

Be careful when using AppendTo and $Assumptions: AppendTo expects a list, but on the first call $Assumptions is just an atomic element (a single element, "True").

I now use the following code to add assumptions to the global $Assumptions:

$Assumptions = Union[Flatten[{$Assumptions, x > 5} ]]

Sharing the internet connection of a Windows machine with a BeagleBone

Let's assume that

• you have a Windows 7 or 8 machine that is connected to the internet via WLAN
• you have an ethernet cable running from your Windows machine to the BeagleBone.
• you want to "share" the internet connection of the Windows machine with the BeagleBone.

The solution: Use "Internet Connection Sharing" (ICS): In the Windows Network Adapter settings, right-click the WLAN adapter, choose "Properties", then go to the "Freigabe" ("Sharing"?) tab and activate the top checkbox that says something about "Allow other computers to use this computer's internet connection". There is a drop-down menu next to it, where you need to choose the ethernet network card.

Note: I got an error last time, something about "can't control adapter settings" or so - I did not write down the error message. This error went away after rebooting the PC.

The Windows computer will then become a sort-of router. It will assign some fixed IP address to your network card (for me it was 192.168.137.1), and it will act as a DHCP server on that network card. But, Windows being Windows, it does not tell you which IP adress it assigns to the BeagleBone!

If you know the network name of you BeagleBone (default: arm), then you should be able to reach it from your windows machine via "arm.mshome.net". If you don't know the network name, you can try to download a network scanner such as this one, and scan the network range from 192.168.137.1 to 192.168.137.255. Two machines should show up: Your own, and the BeagleBone!

Umlauts in Ubuntu

This is a recurring and extremely annoying problem. If you want to (reliably) type Umlauts via PuTTy on a Ubuntu machine, you need to do two things:

On your Windows-machine, make sure that the PuTTy setting "Window"->"Translation" -> "Remote Character Set" is set to "UTF-8".

On your Ubuntu machine that you want to connect to, make sure that the "locale" is set to something UTF-8 compatible.

locale

Gives you the current settings. For me, it used to say a bunch of POSIX stuff. To change that, first do

locale -a

to see the installed locales. If your preferred locale is not there, do

sudo locale-gen en_US.UTF-8
update-locale LANG=en_US.UTF-8

The last command creates a file /etc/default/locale that contains the line LANG=en_US.UTF-8. This environment variable is what sets the locale of your system.

Activating automatic updates

To enable automatic updates on the BeagleBone:

sudo apt-get install unattended-upgrades
sudo dpkg-reconfigure -plow unattended-upgrades

The default options are good: Only apply security upgrades automatically, check once per day. If you want to change these options (I didn't), poke around in

sudo nano /etc/apt/apt.conf.d/50unattended-upgrades
sudo nano /etc/apt/apt.conf.d/20auto-upgrades

Opening it up to the Internet

To make the BeagleBone accessible from the internet, we first have to harden security, and set up dynamic DNS.

Hardening Security

Install fail2ban to ban people who try to log-in with the wrong password too often:

sudo apt-get install fail2ban

You can configure it, if you want, but the default options work nicely.

Disable root login:

sudo nano /etc/ssh/sshd_config

In the section "authentication", make sure that PermitRootLogin is set to "no":

# Authentication:
LoginGraceTime 120
PermitRootLogin no
StrictModes yes

Press ctrl+o, then enter (to save), ctrl+x (to exit).

Restart the ssh server

sudo service ssh restart

Setting up dynamic DNS

You'll need a dynamic DNS provider. There you can sign up for a (free) domain, such as "example.no-ip.com". Using a small utility running either on the BeagleBone or on your router, you can periodically update the domain so that it always points to your (changing) home IP address.

The landscape of dynamic DNS providers keeps changing a bit, but if you look around, you will always find a free provider. One good provider is no-ip.com (if Microsoft isn't blocking them...), another good German provider is spdns.de. I made an account with no-ip.com, but it has the downside that I have to type in a CAPTCHA once a month (they send me an email reminder).

My FritzBox supports no-ip.com directly. Using its admininstrative interface, under "Internet" -> "Shares" -> "DynamicDNS", I can enter my account details. It doesn't take long, and the domain "example123.no-ip.com" (or so) points to the outward-facing IP-address of my FirtzBox.

If your router does not support dynamic DNS, you can download a client for no-ip.com that runs on the BeagleBone. The sudo apt-get ... does not work for current Ubuntu versions, but you can follow the instructions that tell you how to compile it from source. You probably need to install the compiler first:

sudo apt-get install build-essential

Then switch to a root session and download, compile and install the client:

sudo -s
cd /usr/local/src/
wget http://www.no-ip.com/client/linux/noip-duc-linux.tar.gz
tar xf noip-duc-linux.tar.gz
cd noip-2.1.9-1/
make install

You will be asked for your account details. Without exiting the root session, configure the program

/usr/local/bin/noip2 -C

And then start it using

/usr/local/bin/noip2

Finally, exit the root session

exit

Opening ports on the router

This is slightly different for each router, but the general idea is, that you want to tell your router: "If anything arrives at your door on port X, forward it to the machine with the IP-address 192.168.0.Y, port Z.

On the FritzBox, this setting is under "Internet" -> "Shares" -> "Port Shares". Click on "New Port Share". In the "Portshare Active For" dropdown menu, click "Other Shares", and enter the following information:

Name: "ssh" (or whatever you like)
Protocol: "TCP"
From port "22" to port "22"
To computer "manually enter IP adress"
To IP-address "192.168.0.200" (or whatever the IP address of your BeagleBone is)
On port "22"

This forwards the standard ssh port to your BeagleBone. Go to a friend (or install an App on your smartphone and use the cellular network, not WLAN) and try it out by connecting to

ssh bob@example123.no-ip.com

When I try to connect to example123.no-ip.com from my home network, it doesn't work!

If it isn't working, your router might either be so old that it does not support "NAT reflection" (a fancy name for saying: An Internal PC cannot send packets to the external-IP of the router), or it is so new that it tries to prevent "DNS-Rebinding" (an attack technique where the attacker tells your browser to connect to something on the internal network).

The FritzBox tries to prevent "DNS-Rebinding", but you can override this setting for specific domains under "Home Network" -> "Network" -> "Network Settings". Just enter your No-IP.com domain (or whatever dynamic DNS provider you use) into the "DNS rebind protection" box.

Enabling log files

The freshly installed Ubuntu 14.04 on my BeagleBone had another major problem: the logfiles did not work. Doing

ps -ef | grep sys

showed me that the program (daemon) that is responsible for logging, rsyslogd, was running, but when I looked into /var/log, the typical files (such as auth.log) were missing.

My rsyslog.d conf file looked fine, though. I then looked at the configuration of rsyslog. The command

sudo nano /etc/rsyslog.d/50-default.conf

gave me a config file that included the lines

auth,authpriv.*                 /var/log/auth.log
*.*;auth,authpriv.none          -/var/log/syslog

The first line says: Log anything "auth" and "authpriv" related to /var/log/auth.log. The second line says: Log anything, except "auth" and "authpriv" related (the ".none" is supposed to match both "auth" and "authpriv", go figure...) to /var/log/syslog. The minus sign in the latter path tells it not to flush the write buffer or so - I don't know, and I don't care. The configuration looks fine.

So why was logging not working? Answer: Some file permissions were wrong. Doing

ls -la /var/log/

returned, among other lines:

drwxrwxr-x  5 root crontab     4096 Jan  1  1970

That didn't seem right. Although rsyslog.d starts as "root:root", it quickly drops to the user/group "syslog:adm". That user and that group did not have write access to the log directory! So I changed the owner of the log directory:

sudo chown syslog:adm /var/log

and restarted the logging daemon

sudo service rsyslog restart

I tested if it works by logging something nonsensical.

logger hello
sudo nano /var/log/syslog

I saw that the line "hello" was logged, so everything seems to be working. The file /var/log/auth.log already contains evidence of roughly 1 failed login-attempt per 10 seconds. A slightly higher-than-normal rate of hacking attempts.